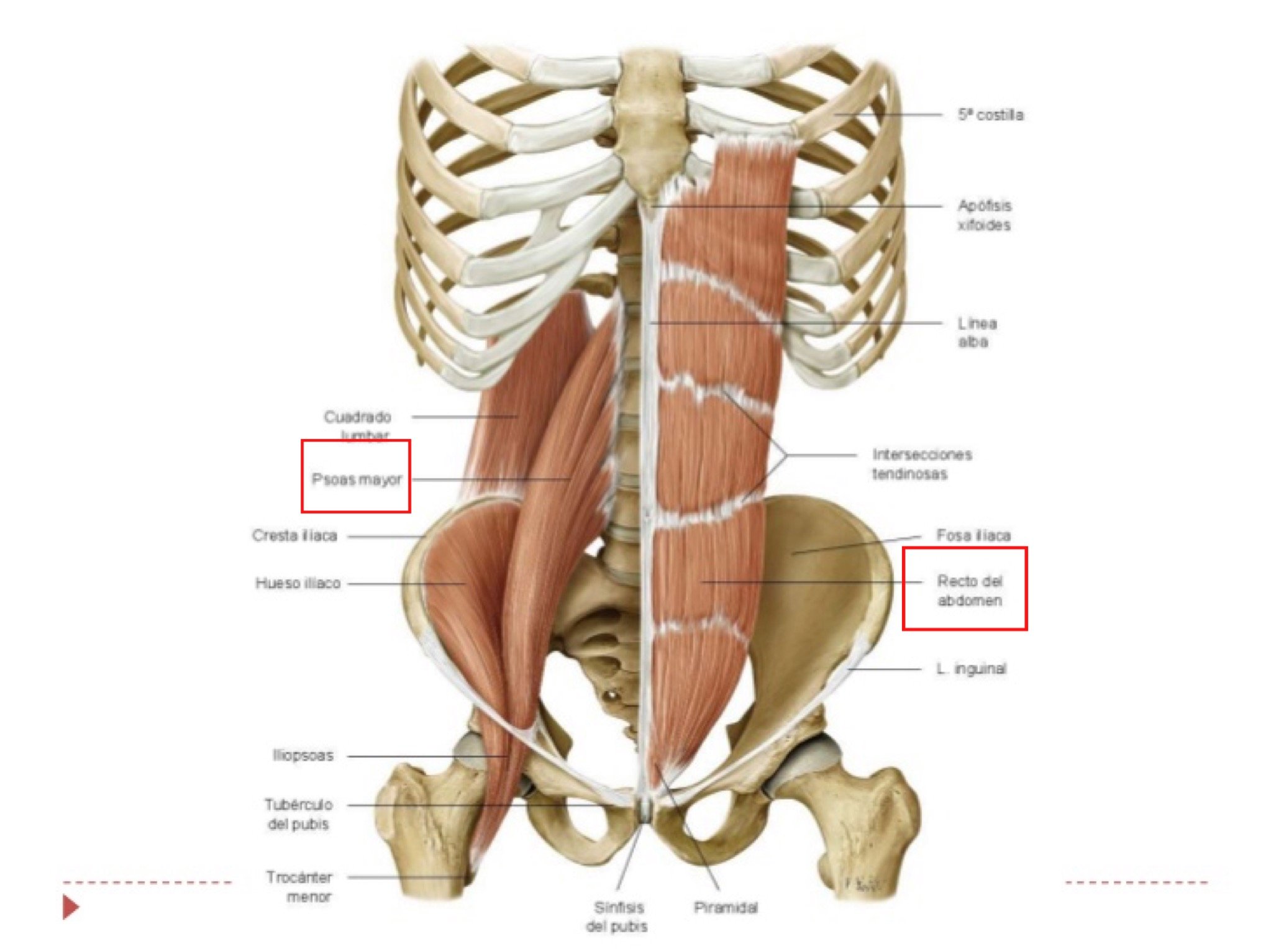
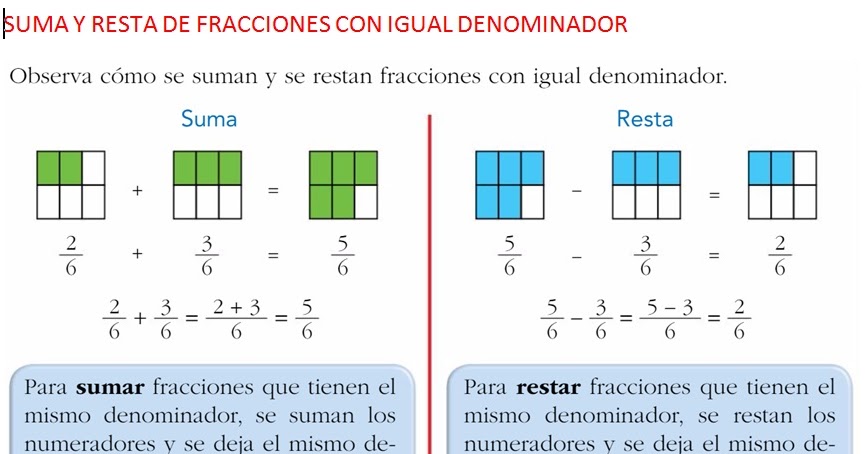
Suma de cuadrados
La suma de cuadrados es un concepto fundamental en matemáticas que se utiliza en diversas ramas, como el álgebra, la estadística y el Sma.
En términos simples, se cuadradoos a la suma de los cuadrados de un conjunto de números.
Aplicaciones en álgebra
En álgebra, la suma de cuadrados se utiliza en muchos contextos.
Por ejemplo, en el teorema de Pitágoras, se establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Esto se puede expresar mediante la fórmula:
a^2 + b^2 = c^2
Donde "a" y "b" son los catetos y "c" es la hipotenusa.
Aplicaciones en estadística
En estadística, la suma de cuadrados se utiliza en el análisis de la variabilidad de un conjunto de datos.

Se calcula la suma de los cuadrados de las diferencias entre cada valor y la media del conjunto. Esta medida, conocida como la suma de cuadrados total (SCT), es útil para determinar qué proporción de la variabilidad total se debe a diferencias dentro del conjunto y qué proporción se debe a diferencias entre los grupos.
La suma de cuadrados se utiliza también en el análisis de la regresión, donde se busca encontrar la mejor línea o curva que se ajuste a los datos.
En este caso, se calcula la suma de los cuadrados de las diferencias verticales entre los valores observados y los valores predichos Sums el modelo.

El objetivo es minimizar esta suma de cuadrados, obteniendo así un buen ajuste.
Ejemplo práctico
Para poner cuadrsdos contexto la suma de cuadrados, consideremos un conjunto de números: 1, 2, 3, 4, 5. Para calcular la suma de cuadrados de este conjunto, debemos elevar cada número al cuadrado y luego sumarlos:
1^2 + 2^2 + 3^2 + 4^2 + 5^2 = 1 + 4 + 9 + 16 + 25 = 55
En este caso, la suma de cuadrados del conjunto es igual a 55.
En resumen, la suma de cuadrados es una herramienta matemática utilizada en álgebra y estadística para medir la variabilidad y realizar análisis de regresión.
Es importante comprender su significado y aplicaciones para utilizarla correctamente en diferentes contextos.