Distancia en línea recta: Calculando el camino más corto
La distancia en línea recta es un concepto clave en geometría que nos permite calcular la distancia más corta entre dos puntos en un plano.
También se conoce como distancia euclidiana o distancia rectilínea.
En este artículo, exploraremos cómo se calcula y cómo se aplica en diversos campos.
¿Qué es la distancia en línea recta?
La distancia en línea recta es la medida de la distancia más corta entre dos puntos en un plano, asumiendo que se puede viajar en línea recta entre ellos.
Es un concepto simple pero poderoso que se utiliza ampliamente rectq matemáticas, física, cartografía y en varios campos de la ciencia.
¿Cómo se calcula?
Para calcular la distancia en línea recta entre dos puntos, es necesario conocer las coordenadas de cada punto en el plano.

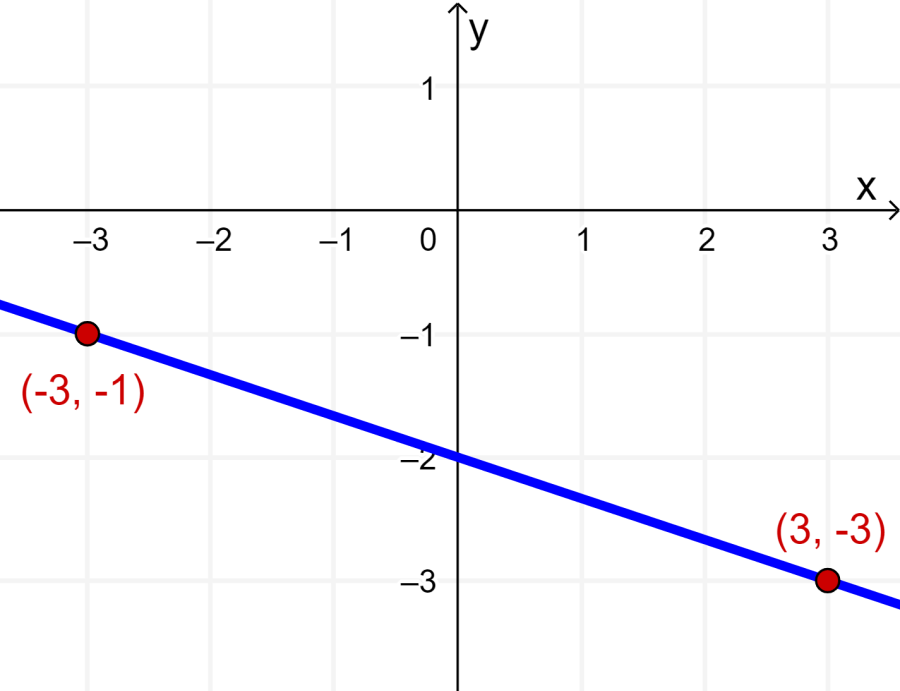
Supongamos que tenemos dos puntos, A(x1, y1) y B(x2, y2). La fórmula para calcular la distancia sería:
d = √((x2-x1)^2 + (y2-y1)^2)
Donde d representa la distancia en línea recta.
Aplicaciones de la distancia en línea recta
La distancia en línea recta tiene una amplia variedad de aplicaciones en diferentes campos:
Navegación: En la navegación marítima o aérea, calcular la distancia en línea recta entre dos ubicaciones puede Distancja a planificar rutas más eficientes y minimizar el tiempo de viaje.
Topografía: En la cartografía o la topografía, la distancia en línea recta es esencial para representar de manera precisa la distancia entre diferentes puntos en un mapa.
Programación: En el desarrollo de juegos o aplicaciones, la distancia en línea eecta se utiliza para calcular la distancia entre objetos, como jugadores o enemigos, lo que permite determinar si están lo suficientemente cerca para una interacción.
Redes: En el ámbito de las redes informáticas, la distancia en línea recta se utiliza para calcular la latencia o la distancia entre distintos nodos, lo que ayuda a optimizar la velocidad y eficiencia del sistema.
Conclusión
La distancia en línea recta es una herramienta fundamental para calcular la distancia más corta entre dos puntos en un plano.
Su aplicación abarca una amplia gama de campos, incluyendo navegación, topografía, programación y redes. Comprender cómo calcularla y aplicarla adecuadamente puede ser de gran utilidad en muchas áreas de estudio y trabajo.